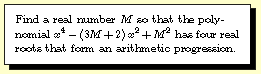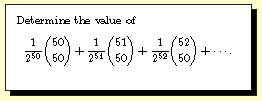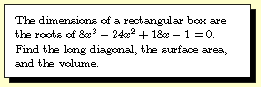... .....	Past Corner Problems: 1999 The problems on display below were all submitted to the Problem Corner during 1999 and then solved by the seven people listed to the right, so they have now been retired and are no longer open questions. Answers to all the problems appear at the end of the page. To see other problems, return to the Problem Corner. ......
	The Problems: The Solvers: Question 1999-1 Attributed to Polya, "How To Solve It" ...... ...... 1) Andrew Dudzik, Lynbrook HS 2) Peter Ruse, Stuyvesant 3) Vladimir Novakovski, TJHSST 4) Richard Eager, TJHSST 5) Gary Sivek, TJHSST 6) Seth Kleinerman, Hunter 7) Abhijit Mehta, Moeller Question 1999-2 Contributed by Melanie Wood ...... ...... 1) Andrew Dudzik, Lynbrook HS 2) Peter Ruse, Stuyvesant 3) Jason Chiu, Laramie HS 4) Vladimir Novakovski, TJHSST 5) Steven Sivek, TJHSST 6) Andrei Simion, Brooklyn Tech 7) Carl Mautner, Miramonte HS   Question 1999-3 Contributed by Peter Ruse ...... ...... 1) Andrew Dudzik, Lynbrook HS 2) Seth Kleinerman, Hunter 3) Vladimir Novakovski, TJHSST 4) Andrei Simion, Brooklyn Tech 5) Richard Eager, TJHSST 6) Kamaldeep Gandhi, Stuyvesant 7) John Huss, Paideia School Question 1999-4 Contributed by Andrew Dudzik ...... ...... 1) Vladmir Novakovski, TJHSST 2) Steven Sivek, TJHSST 3) Richard Eager, TJHSST 4) Steve Byrnes, Roxbury Latin 5) Michiru Kaiou 6) Seth Kleinerman, Hunter 7) Gregory Price, TJHSST Question 1999-5 Contributed by Santo Diano ..... ...... 1) Kamaldeep Gandhi, Stuyvesant 2) Abhijit Mehta, Arch. Moeller 3) Jeremy Miller, S. Douglas 4) Vladmir Novakovski, TJHSST 5) Wing Mui, Brooklyn Tech 6) Steven Sivek, TJHSST 7) Richard Eager, TJHSST Question 1999-6 Contributed by Anthony Phillips ...... ...... 1) Peter Ruse, Stuyvesant 2) Andrew Dudzik, Lynbrook HS 3) Vladimir Novakovski, TJHSST 4) Steve Byrnes, Roxbury Latin 5) Gregory Price, TJHSST 6) John Basias, Brooklyn Tech 7) Richard Eager, TJHSST Question 1999-7 Contributed by Steven Sivek ...... ...... 1) Seth Kleinerman, Hunter 2) Peter Ruse, Stuyvesant 3) Andrei Simion, Brooklyn Tech 4) Vladimir Novakovski, TJHSST 5) Andrew Dudzik, Lynbrook HS 6) Richard Eager, TJHSST 7) Steve Byrnes, Roxbury Latin   Question 1999-8 Contributed by Melanie Wood, also attributed to Crux Mathematicorum ...... ...... 1) Andrew Dudzik, Lynbrook 2) Vladimir Novakovski, TJHSST 3) Seth Kleinerman, Hunter 4) Andrei Simion, Brooklyn Tech 5) Peter Ruse, Stuyvesant 6) Steve Byrnes, Roxbury Latin 7) Jennifer Li, Morgantown   ANSWERS TO 1999 PROBLEMS Question 1999-1 -- there are two possibilities: either M=6 or M=-6/19. Thanks to Steven Sivek of Thomas Jefferson who spotted this one as an exercise in Polya's classic book, How to Solve It. Question 1999-2 -- the sum is 25 C(100,50), i.e. A=25, B=100, and C=50. Question 1999-3 -- the circumradius is R=15. (Hint: the triangle formed by the centers of the three original circles is a right triangle.) Now show that the radius of the small circle nestled between the others and tangent to all three is r=15/29. Question 1999-4 -- the sum is 2, which can be proved by induction or by using the power series expansion for 1/(1-x)^51. Question 1999-5 -- a) 3sqrt(2)/2 b) 9/2 c) 1/8 Along with his solution the proposer included the interesting observation that the roots of the equation are 1+sin(10), 1+sin(50), and 1-sin(70), where the angles are measured in degrees. Can you verify this fact? Question 1999-6 -- in general f(k) equals the number of divisors of k, so the answers are a) f(20)=6 and b) f(k^2)=5 Question 1999-7 -- the total sum is 3/5. One neat approach is to let S be the sum, then compute 9S-3S-S using the Fibonacci recursion to simplify the result. Question 1999-8 -- one quickly conjectures that the product is the square root of three after multiplying them out on a calculator. The proof is left to the reader. ......
	Top of Page | Return to Dialogue | Welcome page