... .....
|
|
|
From 1999 through 2004 there was an active student forum on this page for submitting and solving math problems. Although the forum has been discontinued due to low activity, the nice selection of problems remains for you to enjoy. All are original questions created by high school students. The problems from 2004 appear here, with answers below. The others can be accessed by the links provided. We also encourage students who would like to share some of their own posers to visit The Art of Problem Solving, where there are lively forums for posting and solving original problems.
Previous years:...2003...2002...2001...2000...1999
...
| The Problems:
|
|
| Question 2004-1 |
|
| ...... | |
| Question 2004-2 |
|
| ...... | |
Question 2004-3 submitted by Jesse Geneson |
|
| ...... | |
Question 2004-4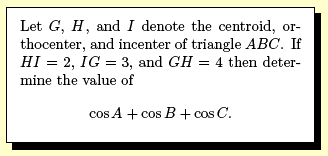 submitted by Thomas Mildorf |
|
| ...... | |
Question 2004-5 submitted by Luke Joyner |
|
| ...... |
ANSWERS TO THE 2004 PROBLEMS
Question 2004-1 One way to
tackle this one is to use the fact that F(1) + F(2) + ... + F(n)
= F(n+2) - 1 repeatedly. You should find that the overall sum
boils down to F(n+4)-n-3
Question 2004-2 It can be done with
just nine pentagons. Try starting with one pentagon at each corner, and
work your way towards the center.
Question 2004-3 The answer is 4, which
can be proved by resorting to inequalities.
Question 2004-4 The answer is 103/94. A brief solution posted
at the Art of Problem Solving web site appears below.
Use standard notation (O is the circumcenter, N the nine-point center, R the circumradius, r the inradius). We know 2 OI^2 = 2R^2 - 4Rr (eqn 1) and that cos A + cos B + cos C = 1 + r/R (eqn 2). We also know that the incircle and the nine-point circle are tangent, so IN = R/2 - r, or 4*IN^2 = R^2 - 4Rr + 4r^2 (eqn 3). Now, we know NOHG are collinear on the Euler line, and that the homothecy about G with factor -1/2 takes H to O and O to N, so GO = 1/2 * GH = 2, GN = 1/2 * GO = 1. Now, use Stewart's theorem to find IN, IO. We get 2^2 * 1 + 3^2 * 3 = 3 * 1 * 4 + 4 IN^2 => 4 IN^2 = 19 (eqn 4), and 3^2 * 6 + 2^2 * -2 = 4 * 6 * -2 + 4 IO^2 => 47 = 2 IO^2 (eqn 5). Now, consider 47(eqn 4) - 19(eqn 5). We get 47 (4 IN^2) - 19 (2 IO^2) = 0. We plug in (eqn 1) and (eqn 3) to find 47 (R^2 - 4Rr + 4r^2) - 19 (2R^2 - 4Rr) = 0 => 9R^2 - 112Rr + 188r^2 = 0 => 188(r/R)^2 - 112(r/R) + 9 = 0 => (2 * (r/R) - 1) * (94 * (r/R) - 9) = 0. The triangle's not equilateral (otherwise all these fun distances would be 0), so we ignore the first factor => r/R = 9/94, so from (eqn 2), we get an answer of 103 / 94.
Question 2004-5 A triangle with sides 1, 2.5, and 2.5 does the job. In general the equation relating a and b will involve a second degree polynomial in these two variables.
......


