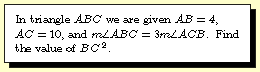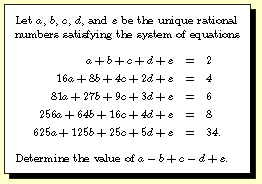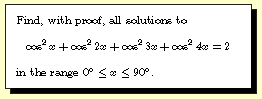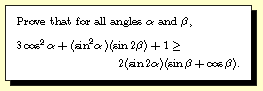... .....	Past Corner Problems: 2001 The problems on display below were all submitted to the Problem Corner during the 2001-02 academic year and then solved by the (up to) seven people listed to the right, so they have now been retired and are no longer open questions. Answers to all the problems appear at the end of the page. To see other problems, return to the Problem Corner. ......
	The Problems: The Solvers: Question 2001-1 submitted by Jaemin Bae, AAST ...... ...... 1) Eve Drucker, AAST 2) Anna Pierrehumbert, ETHS 3) Michel D'Sa, Highland Park 4) Mukund Ramachandran, Cupertino 5) Anatoly Preygel, Mont. Blair 6) Michael Zhang, Stevenson 7) Daniel Herriges, Highland Park Question 2001-2 submitted by Jaemin Bae, AAST ...... ...... 1) Anna Pierrehumbert, ETHS 2) Michel D'Sa, Highland Park 3) Eve Drucker, AAST 4) Frank Kelly, Fort Worth 5) Michael Erlewine, Highland Park 6) Steven Sivek, TJHSST 7) Gary Sivek, TJHSST   Question 2001-3 submitted by Michel D'Sa, Highland Park ...... ...... 1) Steven Sivek, TJHSST 2) Eve Drucker, AAST 3) Anna Pierrehumbert, Evanston 4) Joel Lewis, Stuyvesant 5) Steve Byrnes, Roxbury Latin 6) Jon Pinyan, AAST 7) Al Dracului, Romania Question 2001-4 submitted by Gary Sivek, TJHSST ...... ...... 1) Joel Lewis, Stuyvesant 2) Michel D'Sa, Highland Park 3) Steve Byrnes, Roxbury Latin 4) Anna Pierrehumbert, Evanston 5) Eve Drucker, AAST 6) Jon Pinyan, AAST 7) Michael Erlewine, Highland Park   Question 2001-5 submitted by Steve Byrnes, Roxbury Latin ...... ...... 1) Michel D'Sa, Highland Park Question 2001-6 submitted by Steve Byrnes, Roxbury Latin ...... ...... 1) Eve Drucker, AAST 2) Anna Pierrehumbert, Evanston 3) Michel D'Sa, Highland Park 4) Michael Erlewine, Highland Park 5) Joel Lewis, Stuyvesant 6) Howard Yu, Princeton HS 7) John Mangual, Stuyvesant   Question 2001-7 submitted by Eve Drucker, AAST ...... 1) Howard Yu, Princeton HS 2) Michel D'Sa, Highland Park 3) Jaemin Bae, AAST 4) Steve Byrnes, Roxbury Latin Question 2001-8 submitted by Suleyman Cengiz ...... ...... 1) No solutions submitted   Question 2001-9 submitted by Howard Yu ...... ...... 1) Michel D'Sa, Highland Park 2) Jon Chu, AAST 3) Steve Byrnes, Roxbury Latin ANSWERS TO 2001 PROBLEMS Question 2001-1 -- Use the law of sines to determine that cos2C = 7/8, work from there with law of cosines to obtain BC2=126. Question 2001-2 -- Let f(x)=ax4+bx3+cx2+dx+e, and argue that we must have f(x)=(x-1)(x-2)(x-3)(x-4)+2x. Therefore f(-1)=118, the desired quantity. Question 2001-3 -- By reflecting the figure over successive sides to straighten the path, we find tan(a)=2Sqrt[3] and total path length is Sqrt[13]. Question 2001-4 -- Using a 15-20-25 right triangle we can make the perimeter as small as 80. Question 2001-5 -- One can prove that the largest distance is no more than 72. Can you find a configuration of tunnels and caverns that attains this maximum? Question 2001-6 -- Routine solid geometry formulas along with the Pythagorean theorem produce AB=1980. Question 2001-7 -- This one was tricky. Argue that area(ABC)=15(AB+AC)/2, then use Ptolemy on ABPC and show that BP=PC=5(BC)/8. This leads to area(ABC)=480. Question 2001-8 -- One possible approach is to replace cos2x by (1+cos(2x))/2, and similarly for the other terms, then use a summation formula to reduce the equation to (sin 4x)(cos 5x) / (sin x) = 0, yielding the solutions x=18, 45, 54, or 90 degrees. Question 2001-9 -- Substitute X=(sin a)(sin b), Y=(sin a)(cos b), and Z=cos b to reduce to (X+Y-2Z)2>=0. ......
	Top of Page | Return to Dialogue | Welcome page