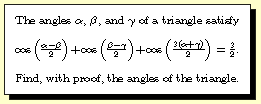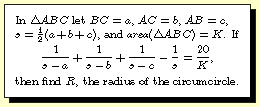... .....	Past Corner Problems: 2000 The problems on display below were all submitted to the Problem Corner during 2000 and then solved by the people listed to the right, so they have now been retired and are no longer open questions. Answers to all the problems appear at the end of the page. To see other problems, return to the Problem Corner. ............
	The Problems: The Solvers: Question 2000-1 submitted by Vladimir Novakovski ........ ...... 1) Andrei Simion, Brooklyn Tech 2) Richard Eager, TJHSST 3) Andrew Dudzik, Lynbrook HS Question 2000-2 submitted by Andrei Simion ........ ...... 1) Vladmir Novakovski, TJHSST 2) Gregory Price, TJHSST 3) Peter Ruse, Stuyvesant 4) Eugene Fridman, Glenbrook N 5) Razvan Visan, Romania Question 2000-3 submitted by Kamaldeep Gandhi ........ ...... 1) Muhammad Atif, Flushing HS 2) Austin Shapiro, Davis HS 3) Nicolo Menez, Bronx HS of Sci Question 2000-4 submitted by David Berger ........ ..... 1) Jeremy Miller, Stoneman Douglas 2) Eugene Fridman, Glenbrook N 3) Mark Bicket, North HS 4) Steve Byrnes, Roxbury Latin 5) Fen Zhao, Hunter College HS 6) Andrei Simion, Brooklyn Tech 7) Charles Wang, IMSA Question 2000-5 submitted by Eugene Fridman ........ ...... 1) Steve Byrnes, Roxbury Latin 2) Jun Lu, Forest Hills 3) Andrei Simion, Brooklyn Tech Question 2000-6 submitted by David Shin ........ ...... 1) Eugene Fridman, Glenbrook N 2) Steve Byrnes, Roxbury Latin 3) Fen Zhao, Hunter College HS Question 2000-7 submitted by Andrew Dudzik ........ ...... 1) Eugene Fridman, Glenbrook N 2) Austin Shapiro, Davis HS 3) John Mangual, Stuyvesant 4) Maria Shah, Hillcrest HS Question 2000-8 submitted by Richard Eager ........ ...... 1) Austin Shapiro, Davis HS 2) Steven Byrnes, Roxbury Latin ANSWERS TO 2000 PROBLEMS Question 2000-1 -- The given sum reduces to 4R/r-2, where R and r are the radii of the circumcircle and incircle, respectively. Therefore the answer is 22. Question 2000-2 -- One conjectures that the cosine of each angle must equal 1/2, leading to the unique solution A=20, B=140, and C=20 degrees. Question 2000-3 -- If we locate point P on side AB of the triangle with PA=3 and PB=4, then arrange for PC to pass through the center of the circumcircle, a limiting value of R=3.7 can be achieved. Question 2000-4 -- First show that the left hand side can be reduced to abc/K^2, where K stands for the area of the triangle. It then follows that R=5. Question 2000-5 -- The given statement implies that the triangle must be a right triangle. (Why?) It is now easy to argue that the maximal area is 25. Question 2000-6 -- An isosceles triangle with sides of length 25, 25, and 30 produces an area of 300, the minimum possible. Question 2000-7 -- The cute answer to this question is {101, 103, 109, 127, 181}. Question 2000-8 -- This question was a difficult exercise in the principle of inclusion-exclusion. There are 7413 even permutations of eight objects with no fixed points. ......
	Top of Page | Return to Dialogue | Welcome page