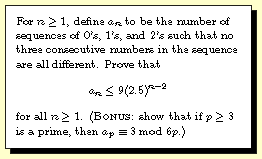... .....	Past Corner Problems: 2003 The problems on display below were all submitted to the Problem Corner during 2003 and then solved by the seven people listed to the right, so they have now been retired and are no longer open questions. Answers to all the problems appear at the end of the page. To see other problems, return to the Problem Corner. ......
	The Problems: The Solvers: ...... Question: 2003-1 submitted by Thomas Mildorf ...... 1) Pinto Sandtelle, Stuyvesant 2) Brian Rice, SWVA Governor's 3) Jon Chu, AAST 4) Ricky Biggs, TJHSST 5) Brian Jacokes, TJHSST 6) Jaemin Bae, AAST 7) Jesse Geneson, TJHSST ...... Question: 2003-2 submitted by Thomas Mildorf ...... 1) Jaemin Bae, AAST 2) Jesse Geneson, TJHSST 3) Jon Chu, AAST 4) Pinto Sandtelle, Stuyvesant 5) Yifei Chen, WWP North 6) Shrenik Shah, Monta Vista 7) John Schulman, Great Neck S ...... Question: 2003-3 submitted by Jaemin Bae ..... 1) Thomas Mildorf, TJHSST 2) Jesse Geneson, TJHSST 3) Jon Chu, AAST 4) Ricky Biggs, TJHSST 5) Thomas Pollom, Cathedral HS 6) Alexei Harvard, Great Neck South 7) John Schulman, Great Neck South ...... Question: 2003-4 submitted by John Schulman ..... 1) Thomas Mildorf, TJHSST 2) Ricky Biggs, TJHSST 3) Brian Rice, SWVA Governor's 4) Pinto Sandtelle, Stuyvesant 5) Thomas Pollom, Cathedral HS 6) Jon Chu, AAST 7) Shrenik Shah, Monta Vista ...... Question: 2003-5 submitted by Thomas Pollom ..... 1) Thomas Mildorf, TJHSST 2) Pinto Sandtelle, Stuyvesant 3) Yifei Chen, WWP North 4) Luke Joyner, Roxbury Latin 5) Jaemin Bae, AAST 6) Ricky Biggs, TJHSST 7) Jeff Chen, TJHSST ...... Question: 2003-6 submitted by Shrenik Shah ..... 1) Jesse Geneson, TJHSST 2) Brian Rice, SW VA Gov 3) Thomas Mildorf, TJHSST 4) Luke Joyner, Roxbury Latin 5) Ricky Biggs, TJHSST 6) Pinto Sandtelle, Stuyvesant 7) Erdem Varol, Stuyvesant ...... Question: 2003-7 submitted by Jesse Geneson ..... 1) Thomas Mildorf, TJHSST 2) Shrenik Shah, Monta Vista HS 3) Albert Ni, IMSA 4) Pinto Sandtelle, Stuyvesant 5) Luke Joyner, Roxbury Latin 6) Ricky Biggs, TJHSST 7) Anthony Kim, TJHSST ...... Question: 2003-8 submitted by Brian Rice ..... 1) Thomas Mildorf, TJHSST 2) Shrenik Shah, Monta Vista HS 3) Jaemin Bae, AAST 4) Pinto Sandtelle, Stuyvesant 5) Hyun-Soo Kim, AAST 6) Jesse Geneson, TJHSST 7) Michael Druker, TJHSST ...... ANSWERS TO 2003 PROBLEMS Question 2003-1 -- the minimum of 5/4 is attained if and only if a=2, b=8, and c=2. To prove this split the third term up into 1/2a + c/4a + c/4a, then use AM-GM on the resulting five terms. Question 2003-2 -- there are many possible ways to find AD; one elegant method involves reflecting point A over line BD to a point A'. One then argues that A' lies on line CD. After working out various other details, one finds that CE = EA' = ED + DA' = ED + AD, which gives AD = 12 - 2*sqrt(14). Question 2003-3 -- the answer is L = 1/6, as shown in the solution sent by the proposer. Question 2003-4 -- there are many different solutions; one simple method is to assign to the point (x,y) the number x. (So that the middle row consists entirely of 0's, the next higher row is all 1's, and so on.) To prove that no such numbering can be periodic, suppose otherwise, and then consider a maximal number in the array. Question 2003-5 -- one such circle is the one with center (0, 6.25) and radius 6.25, passing through the points (0,0), (5,10), (-5,10), (6,8), and (-6,8). The proposer also mentions Schinzel's Theorem, which states that a circle passing through n lattice points is (x-(1/2))^2 + y^2 = (1/4)*5^(k-1) for n = 2k, and (x-(1/3))^2 + y^2 = (1/9)*5^(2k) for n = 2k+1. Question 2003-6 -- write n = t_0 + 3*t_1+9*t_2+...+3^k*t_k in base three, so that each number t_i is either 0, 1, or 2. One then argues that f(n) = t_0 + 2*t_1+4*t_2+...+2^k*t_k. The question then amounts to finding all numbers less than 2003 = 2102022_3 (base three) with only 0's and 1's in their base three representation. All numbers with 7 or less digits and with only 0's and 1's work, so the answer is 128. Question 2003-7 -- the remarkable fact is that one ultimately obtains 1 upon rationalizing the denominator. This may be proven by induction. Question 2003-8 -- First argue that a_(n+1) = 2a_n + a_(n-1). We now proceed by induction. The base cases n=1 and n=2 are trivial. The inductive step is as follows: a_(n+1) = 2a_n + a_(n-1) <= 2*9*(2.5)^(n-2) + 9*(2.5)^(n-3) = 9*(2.5)^(n-3)*(6) < 9*(2.5)^(n-3)*(6.25) = 9*(2.5)^(n-1), as desired. ....
	Top of Page | Return to Dialogue | Welcome page