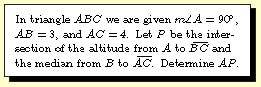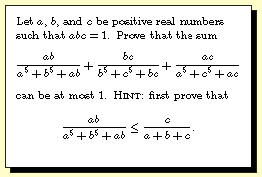... .....	Past Corner Problems: 2002 The problems on display below were all submitted to the Problem Corner during the 2002-03 academic year and then solved by the (up to) seven people listed to the right, so they have now been retired and are no longer open questions. Answers to all the problems appear at the end of the page. To see other problems, return to the Problem Corner. ......
	The Problems: The Solvers: Question 2002-1 Submitted by Jaemin Bae, AAST ...... ...... 1) Pandit Ruse, Stuyvesant 2) Jonathan Gray, Gray Homeschool 3) Eve Drucker, AAST 4) Simon Rubinstein-Salzedo, Homestead 5) Joel Lewis, Stuyvesant 6) Howard Tong, Home School 7) Brian Rice, Marion Sr HS Question 2002-2 Submitted by Joel Lewis, Stuyvesant ...... ...... 1) Matthew Welsh, Stuyvesant 2) Howard Yu, Princeton HS 3) Howard Tong, Tong Home School 4) Jeff Nanney, Clark High School 5) Steve Byrnes, Roxbury Latin 6) Jaemin Bae, AAST 7) Yifei Chen, W.W. Plainsboro North Question 2002-3 Submitted by Matthew Welsh, Stuyvesant ...... ...... 1) Steve Byrnes, Roxbury Latin 2) Joel Lewis, Stuyvesant 3) Andrew Glazer, Glenbrook North 4) Jaemin Bae, AAST 5) Yifei Chen, W.W. Plainsboro North 6) Darwin Candiver, Davis Aerospace 7) Michael Erlewine, Highland Park Sr HS Question 2002-4 Submitted by Steve Byrnes, Roxbury Latin ...... ...... 1) Matthew Welsh, Stuyvesant 2) Brian Rice, Marion Senior HS 3) Darwin Candiver, Davis Aerospace 4) Joel Lewis, Stuyvesant 5) Yifei Chen, W.W. Plainsboro North 6) Jaemin Bae, AAST 7) Jonathan Mizrahi, TJHSST Question 2002-5 Submitted by Anna Pierrehumbert, Evanston Township ...... ...... 1) Matthew Welsh, Stuyvesant 2) Andrew Laitman, Stuyvesant 3) Jaemin Bae, AAST 4) Brian Rice, Marion Sr HS 5) Joel Lewis, Stuyvesant 6) Chris Breaux, Jesuit HS 7) Yifei Chen, W.W. Plainsboro North Question 2002-6 Submitted by Brian Rice, Marion Senior HS ...... ...... 1) Joel Lewis, Stuyvesant 2) Sam Cross, Stuyvesant 3) Darwin Candiver, Davis Aerospace 4) Steve Byrnes, Roxbury Latin Question 2002-7 Submitted by Nick Boatman, Carter High School ...... ...... 1) Matthew Welsh, Stuyvesant 2) Jaemin Bae, AAST 3) Joel Lewis, Stuyvesant 4) Tim Abbott, Thomas Jefferson 5) Atoshi Chowdhury, Baton Rouge 6) Andrew Laitman, Stuyvesant 7) Yifei Chen, W.W. Plainsboro North Question 2002-8 Submitted by a teacher from Kazakstan ...... ...... 1) Matthew Welsh, Stuyvesant 2) Jaemin Bae, AAST 3) Nick Boatman, Carter HS 4) Tim Abbott, Thomas Jefferson 5) Joel Lewis, Stuyvesant 6) Yifei Chen, W.W. Plainsboro North 7) Atoshi Chowdhury, Baton Rouge ANSWERS TO 2002 PROBLEMS Question 2002-1 -- Use your favorite method (Menelaus, for example) to find that AP/PA'=25/9. Then compute AA'=12/5 by finding the area in two different ways to wind up with AP=30/17. Question 2002-2 -- Chase angles in the cyclic quadrilaterals to argue that the only possibility is that all the triangles are equilateral. Hence area(ABC) = 4*Sqrt[3]. Question 2002-3 -- The answer is 2*Sqrt[3]-3. To see why, view the complete solution submitted by the proposer. Question 2002-4 -- The question is equivalent to asking in how many ways six distinguishable objects may be grouped into one or more piles. There are 203 ways to accomplish this. Question 2002-5 -- Use a partial fraction decomposition to rewrite (x-1)/x(x+1)^2 as 2/(x+1)^2+1/(x+1)-1/x. Using the fact that many of the terms in the resulting series cancel, and that 1/1+1/4+1/9+... = Pi^2/6, one obtains the final answer of Pi^2/3-3. Question 2002-6 -- This solution requires some fairly sophisticated combinatorics. We will be content to give the answer, which is C(n, 2)*C(2t, t)/(2^(2t)). Question 2002-7 -- The remainder when P(x) is divided by (x-a)^2 is just (x-a)*P'(a)+P(a). (Can you prove it?) Therefore P(x)=(x-a)^2*Q(x)+(x-a)*P'(a)+P(a), so the answer is 1776x-1549. Question 2002-8 -- The hint follows from the fact that abc=1 and (a^3-b^3)(a^2-b^2)>=0. Similar results hold if we exchange c with either a or b. Adding these three inequalities proves the claim. ......
	Top of Page | Return to Dialogue | Welcome page